The Saturday Paper: Goldilocks And The Three Puzzles

A puzzle, yesterday. With thanks to Gunpoint.

Most procedural generators have it pretty easy. Generation techniques for content like dungeon layouts or 3D worlds can’t really fail – they proceed very steadily, laying down content as they go, and if the occasional tree ends up floating in mid-air it’s not going to break the game. This attitude won’t cut it for more critical game content like puzzles or narratives, however. One small mistake might shortcut half of the plot or render a game trivially easy. How can you tell if a puzzle is solvable in the right way, though? This week on The Saturday Paper we look at how procedural generators can intelligently design puzzles with just the features you want – no more, no less.

We’re reading Quantifying over Play: Constraining Undesirable Solutions in Puzzle Design by Adam Smith, Eric Butler and Zoran Popovic. The paper describes their work investigating AI and game design when building a puzzle designer for the game Refraction 2 (you can play the original for free here), an educational maths puzzle game, and the steps they took to make sure the procedural puzzle generator would not only generate puzzles with particular solutions, but puzzles which didn’t inadvertently have additional, unwanted solutions either. The result is a clever procedural design system that can precisely ensure certain goals are met in its output – something that is completely reusable, and could come in handy in all manner of game design projects.

We’re back in the realm of constraint solving here, which we saw recently when reading about populating dungeons with monsters and items a few weeks back. There’s a longer overview there as well as some links to good tutorials, but the upshot is this: constraint solving lets you describe the results you want from a program, rather than writing the instructions to get there like you would with normal ‘imperative’ programming. If you can find a good representation for your problem – which can be tricky at first – then constraint solvers can rapidly build a solution, making and undoing possible design choices as it tries to match the criteria you give it.

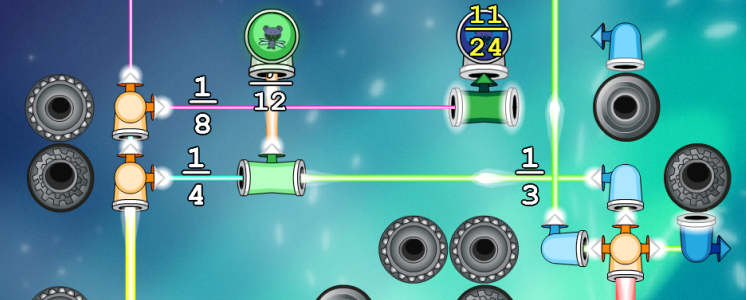
Refraction is a game about understanding fractions. Players place pieces in the path of laser beams to redirect, split, combine or change the beams in some way, in order to provide a particular amount of power to some target spaceships. By allowing the player to split up and combine laser streams the game can test fractional arithmetic and other concepts by designing puzzles that require certain kinds of solution – like merging two 1/16 lasers to power up a spaceship needing 1/8 of power. The authors have already written a paper on a system using constraint solving to design puzzles for this purpose, in fact. So what was their next step?

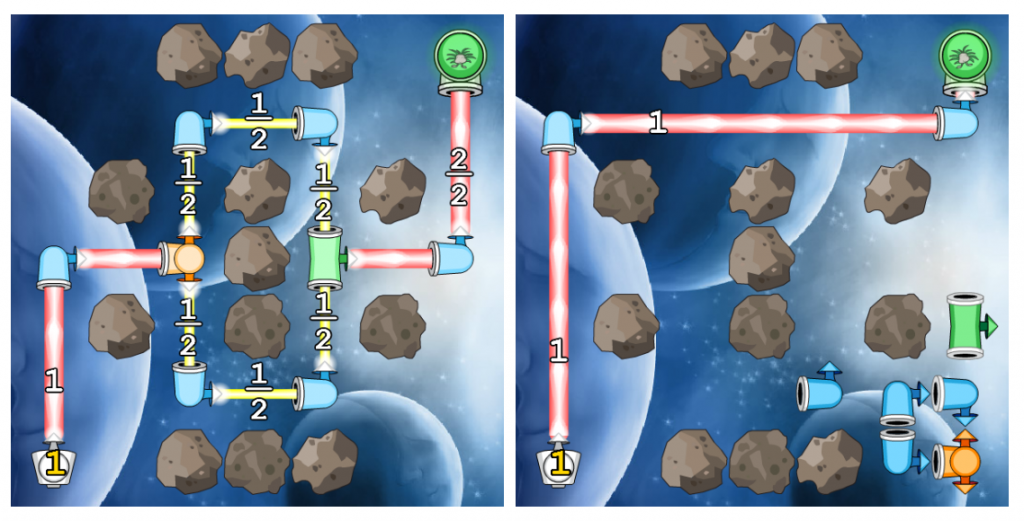
If you look at the picture above, you can see a nice puzzle solution on the left, demonstrating splitting and joining laser beams (with some rather elegantly symmetrical puzzle design to boot), and on the right you can see a nasty shortcut that completely bypasses the whole point of the puzzle. One way to avoid these shortcuts is to generate a puzzle, and then exhaustively test every possible solution to make sure there are no solutions that break the rules you had in mind for this level (such as teaching the player about splitting lasers, as above). This isn’t great for a number of reasons pointed out in the paper – for one thing, this might take ages, especially if the constraints can’t actually be satisfied. Equally importantly, such a system can’t use information about failed designs to stop trying the same idea out for a particular constraint problem.

What if we could express the idea of shortcuts as constraints, just like the rest of the puzzle design system? This would be a huge improvement, because answer set programming (or ASP, the special type of constraint solving used in the paper) improve dramatically over time by using failed solutions to avoid bad designs in future attempts. How do we encode something like that into an ASP, though? The solution uncovered in the paper is initially mind-bending, particularly if you’ve not used ASP before. I’m going to try and give a brief idea here, but I highly recommend reading the paper and contacting the authors to find out more details.

Some puzzles made by the improved solver. Notice how the one on the right doesn’t need rocks at all! It’s all in the elegant placement of the lasers and spaceships.

First, imagine that before we run our solver we give it two things: first, a definition of what we want every solution to include (call it the concept); second, a list of level design features that the solver can define to describe a level. A level design feature might be “Spaceship A needs 1/2 Power” or “There’s a rock at (2,2)”, while a concept might be “The player had to add 1/4 and 1/4 together”. Now suppose our solver comes up with a puzzle-and-solution pair, and through testing it knows it embodies that key concept we want the player to practice. The question is, how do we know if this puzzle has other solutions that pair with it – ones that shortcut our concept?

What we’re looking for (or rather, hoping we don’t find!) is any puzzle-and-solution pair which has exactly the same set of level design features, but that doesn’t have our concept satisfied. If you look at what that means, here’s our initial outcome:

{“Ship needs 1/2 power”, feature2…, featureX, “The player had to add 1/4 and 1/4 together to win”}

And here’s the dastardly shortcut, in which the concept we hoped was required is actually missing:

{“Ship needs 1/2 power”, feature2…, featureX}

In mathematics, the bottom list is a subset of the top list. What Adam and co. do, in just a few lines of ASP, is tell their solver to forbid subsets like this, meaning that if they find them then they know that something about that level design has to change. It’s a little more involved and a lot more clever than I’ve made out, but the principle is the same. And because of the way ASP works, these failures help make the search faster and faster, until a puzzle design is found.

The beauty of this subset checking is that the idea is completely general, and so is the code that Adam and co. have written. As long as you can write down what it means for a concept to be broken or shortcutted for a particular puzzle-and-solution pair, you can use the system developed for Refraction 2 in your own procedural content generator. The paper itself suggests this might be used not just for puzzles, but everything from interactive stories to crafting systems. In essence, it gives developers of procedural generators access to modeling the trickiest problems possible in ASP while staying anchored on the same design task: level design choices and a target concept you wish to see in all player solutions.

Another screen from Gunpoint

The system can produce some really elegant puzzles. As the authors point out, while human designs use things like impassable rocks to block off shortcut solutions (making it much simpler to check the puzzle over visually), the ASP solver is so rigorous it can often satisfy conceptual constraints just by cleverly placing the lasers and their spaceships on the level – and still have a huge diversity of output. I’m really excited to see where this goes next – given that Refraction is a game with education in mind, this could lead to tailored puzzles that teach specific mathematical ideas to people.

I’ve been playing Gunpoint a whole lot since it came out last Monday. In the developer commentary, designer Tom Francis says:

“…if I made the puzzles too open-ended, people found them too easy… then I tried a more restricted version where there was generally only one solution, but people complained it was restrictive … [I ended up with] a puzzle nested within an open-ended level. I found that balance worked much better.”

One of the things I really like about this research – and it’s not exclusive to constraint solving but it’s illustrated so well here – is that with a bit of intelligence in our procedural generators, we could feasibly design puzzles that are perfectly open-ended but where all solutions pass through the same point – exactly as Tom describes his process for Gunpoint worked. Or puzzles where all solutions seem equally feasible (for some definition of ‘feasible’, of course). Or we could design puzzles that explicitly require gadgets the player hasn’t been using very much.

The barrier for many will probably be getting into answer set programming in the first place. The authors here are keen on building better tools, systems and languages that might help developers use the power of ASP without learning a lot of complex new programming ideas though. I originally wrote here, “It’s a barrier worth getting over”, but instead I’ll leave you with a quote from Adam Smith on this very topic, in an email to me about today’s post:

I appreciate your effort in saying “it’s a barrier worth getting over”, but I think I shouldn’t be asking people to cross that particular barrier when I know of not-so-difficult ways to build tunnels through it.

As you can see from the work in their paper, there are some very enticing lights to be seen down the end of this tunnel. I’m looking forward to seeing more of it.

Where To Find More

Adam Smith is currently at the University of Washington in Seattle. He’s extremely friendly and always enthusiastic about getting people thinking in terms of design spaces, just like we did today. If you’re interested in the ideas and technology behind today’s paper, do get in touch with him! Eric Butler is a PhD student at the University of Washington, making games and doing some exciting-sounding research at the same time. Zoran Popovic is at the same university, too – you might recognise his name from the ludicrously impressive Foldit project (which Eric also had a hand in).

In the UK? Come and see Adam Smith talk about his research!

Adam is currently on a trip to the UK, during which time he’s speaking at a few venues. I was lucky enough to be able to invite him to talk at Goldsmiths University on Monday June 17th at 11am, in the New Academic Building (number 2 on this map). All are welcome! The title of Adam’s talk is Mechanizing Exploratory Game Design. Adam is a really inventive and interesting chap and it should be a fantastic talk. Let me know if you’re coming by pinging me on Twitter, where you can also let me know what you thought of this week’s column!

On that note: thanks for reading and for sharing these columns on forums, social media, Reddit and so on. It’s making me really happy to see them being linked to from far and wide, and to see it generating interest and inspiration!

Thanks especially to Darren Grey for once again giving great feedback on the piece, and Adam Smith for helping communicate his work best (he made some great additions to this piece). I’m off to Australia this week for the International Conference on Computational Creativity – when I get back I’m going to do a special roundup episode of The Saturday Paper covering some of the most interesting creative research and how it could be used inside games.